matlab连续系统离散化, 零阶保持器法

MATLAB连续系统离散化方法详解

在控制工程和信号处理领域，连续系统离散化是一个重要的步骤。将连续系统转换为离散系统，可以方便地使用数字计算机进行仿真和控制。MATLAB作为一种强大的数学计算软件，提供了多种连续系统离散化的方法。本文将详细介绍MATLAB中常用的连续系统离散化方法，包括零阶保持器法、一阶保持器法、双线性变换法等。

零阶保持器法

零阶保持器法（Zero-Order Hold, ZOH）是一种常用的连续系统离散化方法。它假设在采样时刻，连续信号保持不变，直到下一个采样时刻。在MATLAB中，可以使用`c2d`函数实现零阶保持器法离散化。

```matlab

% 示例：使用零阶保持器法离散化一个连续系统

sys = tf(1, [1 2 3]); % 定义一个连续系统

Ts = 0.1; % 采样周期

sysd = c2d(sys, Ts, 'zoh'); % 使用零阶保持器法离散化

一阶保持器法

一阶保持器法（First-Order Hold, FOH）与零阶保持器法类似，但它假设在采样时刻，连续信号的变化率保持不变。在MATLAB中，可以使用`c2d`函数实现一阶保持器法离散化。

```matlab

% 示例：使用一阶保持器法离散化一个连续系统

sys = tf(1, [1 2 3]); % 定义一个连续系统

Ts = 0.1; % 采样周期

sysd = c2d(sys, Ts, 'foh'); % 使用一阶保持器法离散化

双线性变换法

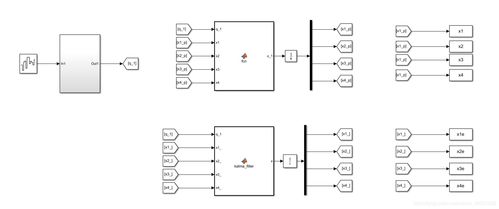
双线性变换法（Tustin's Method）是一种常用的连续系统离散化方法，它通过将s域的拉普拉斯变换转换为z域的Z变换来实现。在MATLAB中，可以使用`c2d`函数实现双线性变换法离散化。

```matlab

% 示例：使用双线性变换法离散化一个连续系统

sys = tf(1, [1 2 3]); % 定义一个连续系统

Ts = 0.1; % 采样周期

sysd = c2d(sys, Ts, 'tustin'); % 使用双线性变换法离散化

改进的双线性变换法

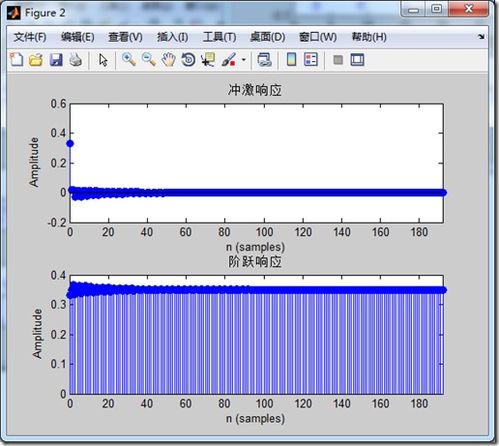
改进的双线性变换法（Prewarp Tustin's Method）是一种改进的双线性变换法，它通过预扭曲s平面来提高离散化后的系统性能。在MATLAB中，可以使用`c2d`函数实现改进的双线性变换法离散化。

```matlab

% 示例：使用改进的双线性变换法离散化一个连续系统

sys = tf(1, [1 2 3]); % 定义一个连续系统

Ts = 0.1; % 采样周期

sysd = c2d(sys, Ts, 'prewarp'); % 使用改进的双线性变换法离散化

零极点匹配法

零极点匹配法（Zero-Pole Matching Method）是一种通过匹配连续系统和离散系统零极点的方法来实现离散化。在MATLAB中，可以使用`c2d`函数实现零极点匹配法离散化。

```matlab

% 示例：使用零极点匹配法离散化一个连续系统

sys = tf(1, [1 2 3]); % 定义一个连续系统

Ts = 0.1; % 采样周期

sysd = c2d(sys, Ts, 'matched'); % 使用零极点匹配法离散化

MATLAB提供了多种连续系统离散化的方法，包括零阶保持器法、一阶保持器法、双线性变换法等。根据实际应用需求，可以选择合适的离散化方法来实现连续系统的离散化。通过MATLAB的`c2d`函数，可以方便地将连续系统转换为离散系统，为后续的仿真和控制设计提供基础。