matlab 系统聚类分析

MATLAB系统聚类分析：方法、应用与实例

摘要

系统聚类分析是一种常用的数据挖掘和统计分析方法，它通过将数据集中的对象按照一定的相似性准则进行分组，从而揭示数据中的内在结构。MATLAB作为一种强大的科学计算软件，提供了丰富的工具和函数，可以方便地进行系统聚类分析。本文将介绍MATLAB系统聚类分析的基本方法、应用场景以及一个具体的实例分析。

一、系统聚类分析概述

系统聚类分析是一种无监督学习的方法，它通过将数据集中的对象按照一定的相似性准则进行分组，从而揭示数据中的内在结构。常见的相似性准则包括距离度量（如欧氏距离、曼哈顿距离等）和相似系数（如相关系数、夹角余弦等）。

二、MATLAB系统聚类分析的基本方法

在MATLAB中，可以使用以下步骤进行系统聚类分析：

导入数据：使用MATLAB的导入函数（如readtable、readmatrix等）将数据导入到工作空间。

计算相似性矩阵：使用MATLAB的相似性计算函数（如pdist、dist等）计算数据集中对象之间的相似性矩阵。

选择聚类方法：根据数据特点和需求选择合适的聚类方法，如层次聚类、K均值聚类等。

执行聚类分析：使用MATLAB的聚类分析函数（如linkage、kmeans等）进行聚类分析。

结果可视化：使用MATLAB的可视化函数（如scatter、plot等）将聚类结果可视化。

三、MATLAB系统聚类分析的应用场景

市场细分：通过对消费者数据的聚类分析，将消费者划分为不同的市场细分群体。

客户关系管理：通过对客户数据的聚类分析，识别出具有相似特征的客户群体，从而进行更有针对性的营销策略。

生物信息学：通过对基因表达数据的聚类分析，发现基因之间的相互作用和调控关系。

图像处理：通过对图像数据的聚类分析，识别出图像中的不同区域和特征。

四、实例分析：基于MATLAB的系统聚类分析

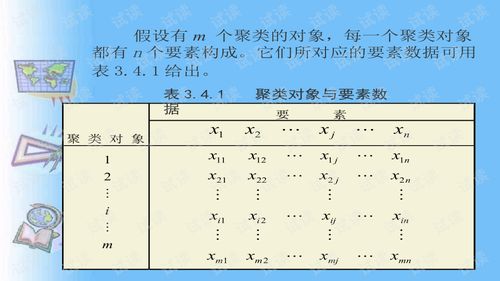
以下是一个基于MATLAB的系统聚类分析实例，我们将使用一个简单的二维数据集进行聚类分析。

1. 数据导入

首先，我们需要导入数据集。假设数据集包含两个特征（x和y）和对应的样本值，数据存储在CSV文件中。

data = readtable('data.csv');

2. 计算相似性矩阵

接下来，我们计算数据集中对象之间的相似性矩阵。这里我们使用欧氏距离作为相似性度量。

distances = pdist(data{:, [1, 2]}, 'euclidean');

3. 选择聚类方法

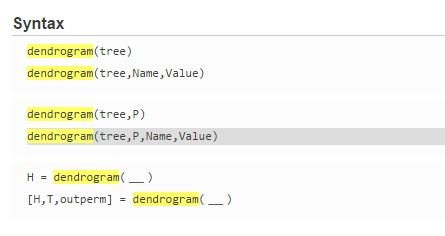
在本例中，我们选择层次聚类方法进行聚类分析。

clusters = linkage(distances, 'complete');

4. 执行聚类分析

使用MATLAB的cluster函数进行聚类分析，并设置聚类数量为2。

num_clusters = 2;

cluster_labels = cluster(clusters, num_clusters);

5. 结果可视化

我们将聚类结果可视化，以便更好地理解聚类效果。

figure;

scatter(data{:, 1}, data{:, 2}, cluster_labels, 'filled');

xlabel('Feature 1');

ylabel('Feature 2');

title('Cluster Analysis Result');

本文介绍了MATLAB系统聚类分析的基本方法、应用场景以及一个具体的实例分析。通过MATLAB的强大功能，我们可以方便地进行系统聚类分析，并揭示数据中的内在结构。在实际应用中，可以根据具体问题和数据特点选择合适的聚类方法和相似性度量，从而获得更好的聚类效果。

关键词

系统聚类分析；MATLAB；层次聚类；相似性矩阵；数据挖掘