mm1排队系统

什么是M/M/1排队系统？

M/M/1排队系统是排队论中的一个经典模型，它描述了一个单服务台、顾客到达和服务时间均服从指数分布的排队系统。在这个模型中，“M”代表顾客到达时间服从指数分布，“M”同样代表服务时间服从指数分布，“1”代表系统中只有一个服务台。

M/M/1排队系统的基本假设

M/M/1排队系统基于以下基本假设：

顾客到达时间服从参数为λ的指数分布，即顾客到达的平均间隔为1/λ。

服务时间服从参数为μ的指数分布，即服务一个顾客的平均时间为1/μ。

系统容量无限，即顾客可以无限排队等待服务。

顾客到达和服务过程相互独立。

M/M/1排队系统的性能指标

M/M/1排队系统的主要性能指标包括：

利用率（ρ）：ρ = λ / μ，表示服务台被占用的比例。

平均排队长度（Lq）：Lq = ρ^2 / (1 - ρ)，表示在稳态下平均排队等待的顾客数量。

平均等待时间（Wq）：Wq = Lq / λ，表示在稳态下顾客平均等待服务的时间。

平均系统中的顾客数（L）：L = Lq + ρ，表示在稳态下系统中平均的顾客数量。

平均服务时间（W）：W = 1 / μ，表示在稳态下顾客平均接受服务的时间。

M/M/1排队系统的应用

银行柜台服务：分析银行柜员的工作效率和服务质量。

电话客服中心：评估客服人员的数量和服务水平。

医院挂号处：优化挂号流程，减少患者等待时间。

交通信号灯控制：优化交通流量，减少车辆等待时间。

M/M/1排队系统的优化方法

为了提高M/M/1排队系统的性能，可以采取以下优化方法：

调整服务台数量：根据需求增加或减少服务台数量，以降低顾客等待时间。

优化服务流程：简化服务流程，提高服务效率。

调整到达率：通过营销策略或调整营业时间，控制顾客到达率。

引入优先级机制：对顾客进行分类，优先服务重要顾客。

M/M/1排队系统的仿真分析

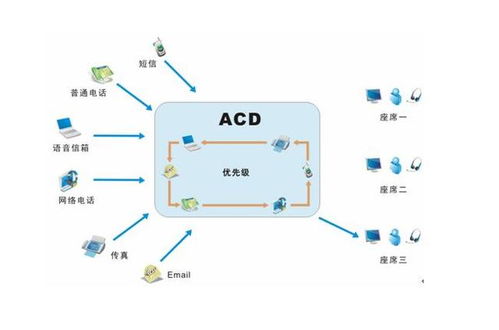
使用排队论软件：如Queueing Network Analyzer（QNA）等软件，可以方便地进行M/M/1排队系统的仿真分析。

编写仿真程序：使用编程语言（如Python、MATLAB等）编写仿真程序，模拟排队系统的运行过程。

分析仿真结果：根据仿真结果，评估排队系统的性能指标，并提出优化建议。

M/M/1排队系统是排队论中的一个重要模型，它可以帮助我们分析和优化各种排队系统。通过了解M/M/1排队系统的基本假设、性能指标和应用场景，我们可以更好地解决实际问题，提高系统效率和服务质量。