lti系统,LTI系统的定义与特性

线性时不变（Linear Time-Invariant，LTI）系统是信号与系统理论中的一个重要概念。在通信、控制、图像处理等领域，LTI系统扮演着核心角色。本文将详细介绍LTI系统的基本概念、特性以及分析方法，旨在帮助读者更好地理解和应用LTI系统。

LTI系统的定义与特性

LTI系统是指输入信号的线性组合等于输出信号的线性组合，且系统的参数不随时间变化的系统。具体来说，如果系统T对输入信号x(n)的输出为y(n)，那么对于任意常数a和b，以及任意输入信号x1(n)和x2(n)，有：

y(n) = T[x(n)] = aT[x1(n)] + bT[x2(n)]

其中，a和b为任意常数。

LTI系统的特性主要包括以下两点：

线性：系统对输入信号的响应是线性的，即输出信号是输入信号的线性组合。

时不变：系统的参数不随时间变化，即系统在任意时刻的响应与在任意时刻的响应相同。

LTI系统的数学描述

LTI系统的数学描述主要有以下几种形式：

差分方程：对于离散信号，LTI系统可以用差分方程来描述。例如，一个一阶LTI系统的差分方程可以表示为：

y(n) = a1y(n-1) + b0x(n) + b1x(n-1)

微分方程：对于连续信号，LTI系统可以用微分方程来描述。例如，一个二阶LTI系统的微分方程可以表示为：

y''(t) + 2ay'(t) + by(t) = ax'(t) + bx(t)

传递函数：传递函数是LTI系统的一个重要数学工具，它描述了系统输入与输出之间的关系。对于离散信号，传递函数可以表示为：

H(z) = Y(z)/X(z)

频率响应：频率响应描述了系统对不同频率信号的响应。对于离散信号，频率响应可以表示为：

H(e^(jω)) = Y(e^(jω))/X(e^(jω))

LTI系统的分析方法

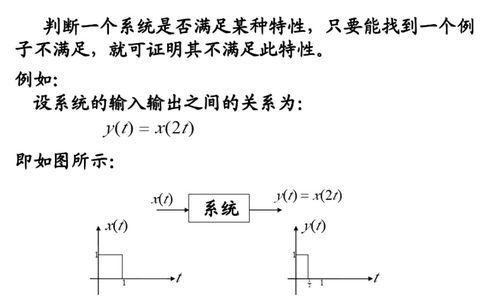
LTI系统的分析方法主要包括以下几种：

时域分析：时域分析是直接对系统的时间响应进行分析。例如，通过求解差分方程或微分方程，可以得到系统在不同输入信号下的输出信号。

变换域分析：变换域分析是将信号和系统从时域转换到变换域（如Z域、傅里叶域）进行分析。在变换域中，信号和系统的处理更加方便，例如，可以通过求解传递函数来分析系统的频率响应。

频域分析：频域分析是分析系统对不同频率信号的响应。通过频率响应，可以了解系统的滤波特性、稳定性等。

LTI系统的应用

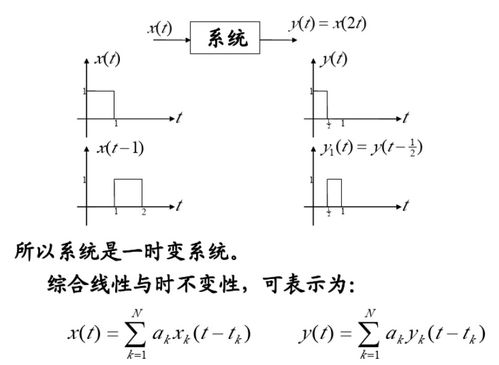
LTI系统在各个领域都有广泛的应用，以下列举几个例子：

通信系统：在通信系统中，LTI系统用于信号调制、解调、滤波等。

控制系统：在控制系统中，LTI系统用于控制器设计、系统稳定性分析等。

图像处理：在图像处理中，LTI系统用于图像滤波、边缘检测等。

线性时不变（LTI）系统是信号与系统理论中的一个重要概念，具有广泛的应用。本文介绍了LTI系统的基本概念、特性、数学描述以及分析方法，旨在帮助读者更好地理解和应用LTI系统。在实际应用中，根据具体问题选择合适的方法进行分析和设计，可以有效地解决各种信号与系统问题。