n复杂系统,什么是n复杂系统

随着科学技术的飞速发展，复杂系统在自然界、社会和工程领域扮演着越来越重要的角色。复杂系统通常由大量相互作用的元素组成，这些元素之间的相互作用和反馈机制使得系统的行为表现出高度的非线性、不确定性和复杂性。本文将探讨n复杂系统的概念、特点以及研究方法，旨在为理解和解决复杂系统问题提供新的视角。

什么是n复杂系统

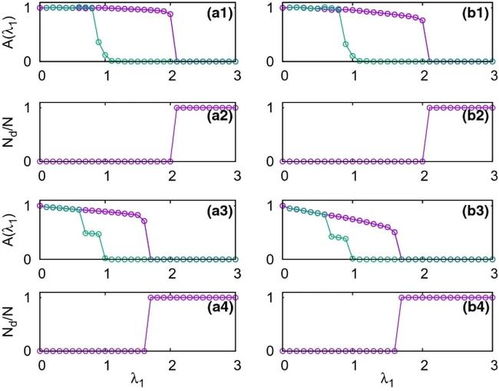
在复杂系统理论中，n复杂系统指的是由n个或更多相互作用的元素组成的系统。这些元素可以是物理实体、生物个体、社会个体或抽象概念。n复杂系统的特点在于其元素之间的复杂相互作用和反馈机制，导致系统表现出非线性、涌现性和自组织等特性。

n复杂系统的特点

1. 非线性：n复杂系统中，元素之间的相互作用通常是非线性的，即系统行为与输入之间存在非线性关系。这种非线性使得系统难以用传统的线性模型进行描述和分析。

2. 涌现性：n复杂系统中的元素相互作用会产生新的结构和功能，这些结构和功能在单个元素层面上并不存在。这种现象被称为涌现性，是n复杂系统的重要特征。

3. 自组织：n复杂系统中的元素会根据系统内部和外部的信息进行自我调整和优化，以适应环境变化。这种自组织能力使得系统具有高度适应性和灵活性。

4. 不确定性：n复杂系统中的元素相互作用和反馈机制可能导致系统行为的不确定性，使得预测系统未来状态变得困难。

n复杂系统的研究方法

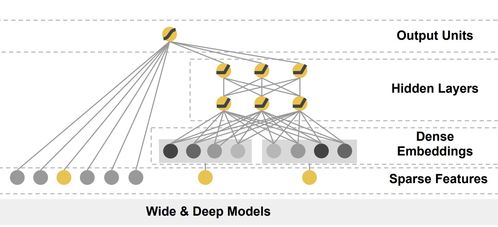
1. 系统动力学：系统动力学是研究n复杂系统动态行为的一种方法，通过建立系统模型来模拟和分析系统行为。系统动力学模型通常采用微分方程或差分方程来描述系统状态变量随时间的变化。

2. 复杂网络理论：复杂网络理论是研究n复杂系统中元素之间相互作用关系的一种方法。通过构建网络模型，可以分析系统中的关键节点、网络拓扑结构以及网络演化规律。

3. 涌现理论：涌现理论是研究n复杂系统中涌现现象的一种方法。通过分析系统元素之间的相互作用和反馈机制，揭示涌现现象的产生机制。

4. 机器学习与数据挖掘：随着大数据时代的到来，机器学习与数据挖掘技术为n复杂系统研究提供了新的手段。通过分析大量数据，可以发现系统中的规律和模式，为系统优化和决策提供支持。

n复杂系统的应用

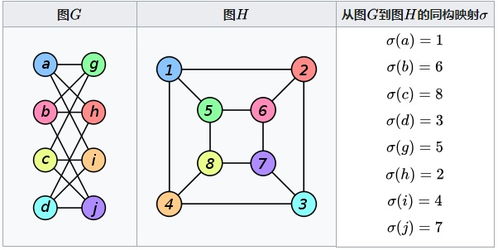
1. 生物系统：n复杂系统理论在生物学领域有着广泛的应用，如研究生态系统、细胞网络、神经网络等。

2. 社会系统：n复杂系统理论在社会学、经济学、政治学等领域也有着重要的应用，如研究城市交通、金融市场、社会网络等。

3. 工程系统：n复杂系统理论在工程领域也有着广泛的应用，如研究电力系统、通信系统、交通系统等。

结论

n复杂系统作为一种高度非线性和不确定性的系统，具有丰富的科学内涵和应用价值。随着科学技术的不断发展，n复杂系统研究将不断深入，为解决现实世界中的复杂问题提供有力支持。