matlab系统时间,深入理解时域与频域的关系

MATLAB系统时间分析：深入理解时域与频域的关系

在信号与系统领域，MATLAB作为一种强大的工具，被广泛应用于时域和频域的分析。本文将深入探讨MATLAB在系统时间分析中的应用，包括时域分析、频域分析以及两者之间的关系。

一、时域分析

时域分析是信号与系统分析的基础，它关注信号和系统在时间轴上的变化。在MATLAB中，我们可以通过以下几种方法进行时域分析：

1.1 信号描述与分类

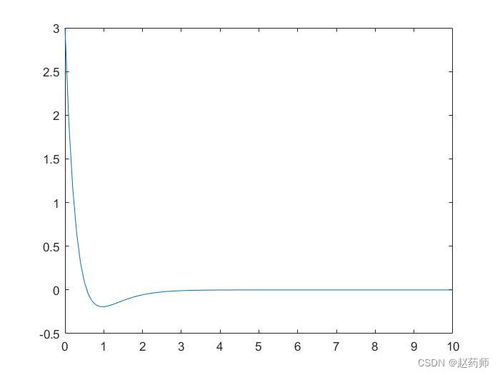
在MATLAB中，我们可以使用多种函数来描述和分类信号。例如，使用`plot`函数可以绘制信号的波形图，使用`fft`函数可以计算信号的快速傅里叶变换（FFT），从而得到信号的频谱。

1.2 信号的基本运算及特性

在MATLAB中，我们可以对信号进行各种基本运算，如加、减、乘、除等。此外，我们还可以分析信号的特性，如幅度、相位、频率等。

1.3 信号的分解

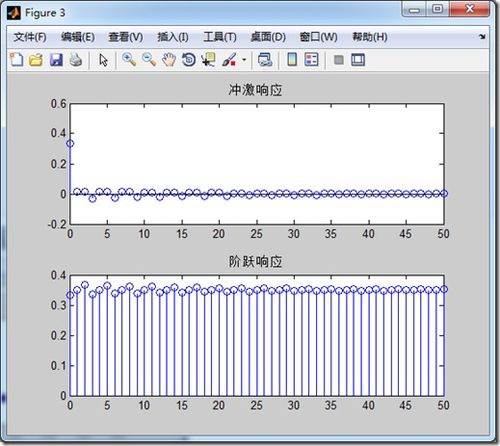
在MATLAB中，我们可以将信号分解为多个分量，如交直流分量、冲激函数分量、阶跃函数分量等。这有助于我们更好地理解信号的组成和特性。

二、频域分析

频域分析关注信号和系统在频率域上的变化。在MATLAB中，我们可以通过以下几种方法进行频域分析：

2.1 傅里叶变换

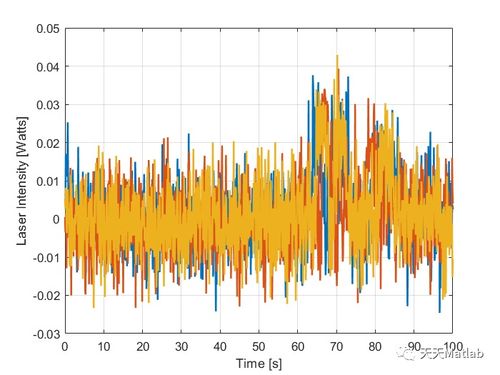
傅里叶变换是信号与系统分析中的核心工具。在MATLAB中，我们可以使用`fft`函数进行快速傅里叶变换，将时域信号转换为频域信号，从而分析信号的频率成分。

2.2 傅里叶级数

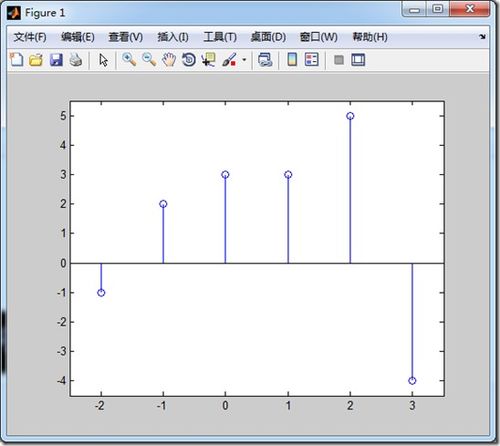
对于周期信号，我们可以使用傅里叶级数进行分析。在MATLAB中，我们可以使用`fft`函数和`ifft`函数进行傅里叶变换和逆变换，从而分析信号的频率成分。

2.3 傅里叶变换的性质

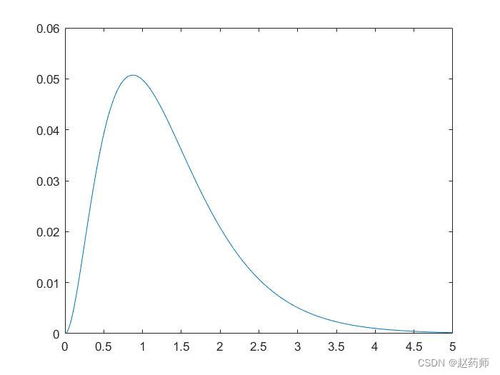
在MATLAB中，我们可以利用傅里叶变换的性质，如时移、频移、尺度变换等，对信号进行操作和分析。

三、时域与频域的关系

3.1 傅里叶变换的时域与频域表示

傅里叶变换将时域信号转换为频域信号，从而揭示了信号在频率域上的分布。在MATLAB中，我们可以通过`fft`函数和`ifft`函数进行傅里叶变换和逆变换，从而分析信号的时域和频域表示。

3.2 时域卷积与频域乘积

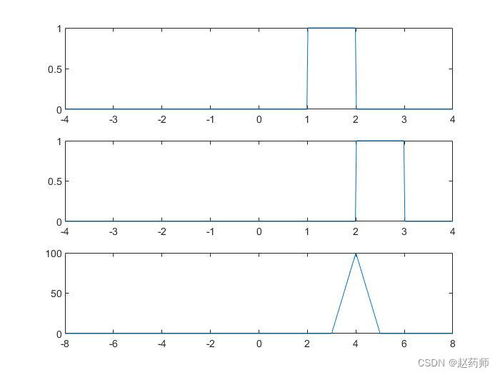
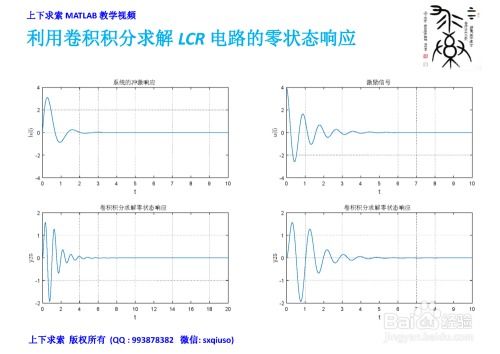
时域卷积和频域乘积是信号与系统分析中的两个重要概念。在MATLAB中，我们可以利用`conv`函数进行时域卷积，利用`fft`函数和`ifft`函数进行频域乘积，从而分析信号和系统的时域与频域关系。

3.3 系统的频率响应

系统的频率响应描述了系统在不同频率下的响应特性。在MATLAB中，我们可以使用`freqz`函数计算系统的频率响应，从而分析系统的时域与频域关系。

四、MATLAB在系统时间分析中的应用

在MATLAB中，我们可以通过以下几种方法进行系统时间分析：

4.1 系统的零状态响应

在MATLAB中，我们可以使用`lsim`函数求解连续时间系统的零状态响应。该函数可以绘制系统在输入信号作用下的零状态响应波形。

4.2 系统的单位冲激响应

在MATLAB中，我们可以使用`impulse`函数求解连续时间系统的单位冲激响应。该函数可以绘制系统在单位冲激信号作用下的响应波形。

4.3 系