matlab线性系统,线性系统建模

线性系统在工程、物理、经济等多个领域都有着广泛的应用。MATLAB作为一种强大的数学计算软件，提供了丰富的工具和函数来分析和设计线性系统。本文将介绍MATLAB在线性系统分析中的应用，包括系统建模、时域分析、频域分析以及控制器设计等方面。

线性系统建模

在MATLAB中，线性系统的建模可以通过传递函数、状态空间模型或零极点增益模型来实现。

传递函数模型：使用`tf`函数创建传递函数模型，例如：

sys = tf([1 2 3], [1 0.5 0.25]);

状态空间模型：使用`ss`函数创建状态空间模型，例如：

sys = ss([1 0 0; 0 1 0; 0 0 1], [0 1 0; 0 0 1], [0 0 0], [1 0 0]);

零极点增益模型：使用`zpk`函数创建零极点增益模型，例如：

sys = zpk([1 -1], [1 0.5], 1);

时域分析

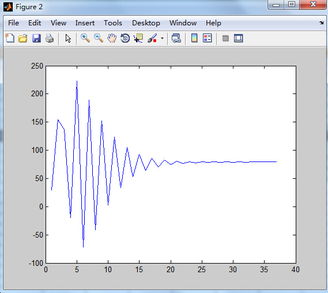
时域分析是研究线性系统在时间域内的行为。在MATLAB中，可以使用以下函数进行时域分析：

单位阶跃响应：使用`step`函数，例如：

step(sys);

单位脉冲响应：使用`impulse`函数，例如：

impulse(sys);

单位斜坡响应：使用`ramp`函数，例如：

ramp(sys);

频域分析

频域分析是研究线性系统在频率域内的行为。在MATLAB中，可以使用以下函数进行频域分析：

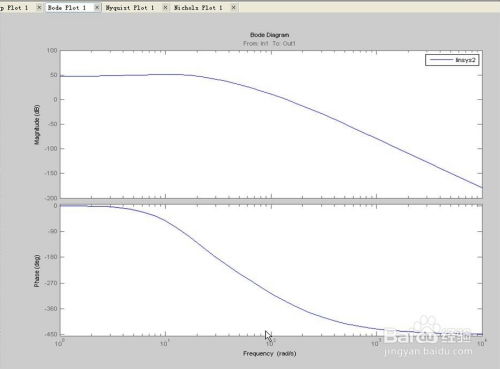
伯德图：使用`bode`函数，例如：

bode(sys);

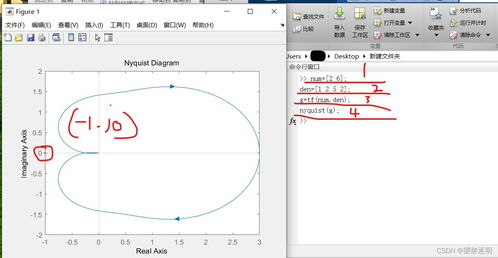
奈奎斯特图：使用`nyquist`函数，例如：

nyquist(sys);

频率响应：使用`freqresp`函数，例如：

freqresp(sys, logspace(-2, 2, 100));

控制器设计

控制器设计是线性系统分析中的重要环节。在MATLAB中，可以使用以下方法进行控制器设计：

PID控制器：使用`pid`函数创建PID控制器，例如：

pidCtrl = pid(1, 1, 1);

状态反馈控制器：使用`place`函数进行状态反馈控制器设计，例如：

place(sys, [1 0 0], [1 0 0]);

根轨迹分析：使用`rlocus`函数进行根轨迹分析，例如：

rlocus(sys);

结论

本文介绍了MATLAB在线性系统分析中的应用，包括系统建模、时域分析、频域分析以及控制器设计等方面。通过MATLAB的强大功能，我们可以方便地进行线性系统的分析和设计，为工程实践提供有力支持。

线性系统，MATLAB，时域分析，频域分析，控制器设计