matlab二阶系统的阶跃响应,二阶系统的基本概念

在自动控制系统中，二阶系统因其广泛的应用而备受关注。二阶系统的阶跃响应是评估其动态性能的重要手段。本文将利用MATLAB软件对二阶系统的阶跃响应进行分析，探讨系统参数对响应的影响，并展示如何通过MATLAB进行仿真实验。

二阶系统的基本概念

二阶系统是指具有两个独立能控能观状态的一阶线性时不变系统。其传递函数通常表示为：

[ G(s) = frac{omega_n^2}{s^2 + 2zetaomega_ns + omega_n^2} ]

其中，(omega_n)为无阻尼自然频率，(zeta)为阻尼比。二阶系统的阶跃响应主要取决于这两个参数。

阶跃响应的MATLAB仿真

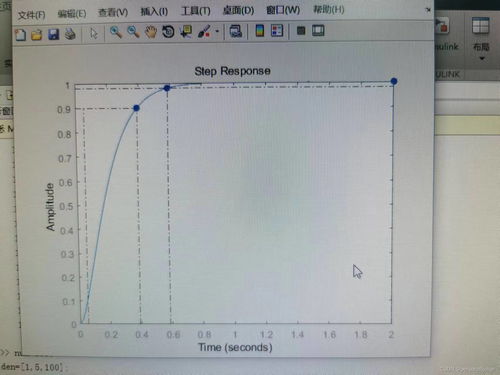
在MATLAB中，我们可以使用控制系统工具箱中的`step`函数来绘制二阶系统的阶跃响应曲线。以下是一个简单的示例代码：

```matlab

% 定义系统参数

wn = 5; % 无阻尼自然频率

zeta = 0.7; % 阻尼比

% 定义传递函数

num = wn^2;

den = [1 2zetawn wn^2];

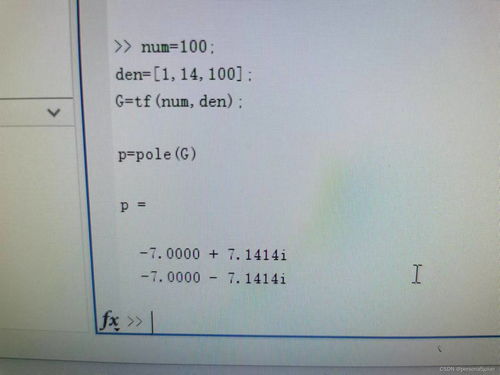
G = tf(num, den);

% 绘制阶跃响应曲线

step(G);

运行上述代码后，将得到一个二阶系统的阶跃响应曲线。通过调整`wn`和`zeta`的值，我们可以观察系统参数对响应的影响。

系统参数对阶跃响应的影响

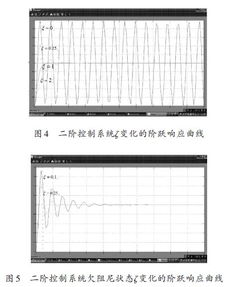
以下将分别讨论无阻尼自然频率和阻尼比对阶跃响应的影响。

无阻尼自然频率的影响

无阻尼自然频率(omega_n)决定了系统的快速性和稳定性。当(omega_n)增大时，系统的上升时间缩短，但超调量可能增大。以下是一个示例代码，展示了不同(omega_n)值对阶跃响应的影响：

```matlab

% 定义不同无阻尼自然频率

wn_values = [2, 5, 10];

% 循环绘制阶跃响应曲线

for i = 1:length(wn_values)

wn = wn_values(i);

num = wn^2;

den = [1 2zetawn wn^2];

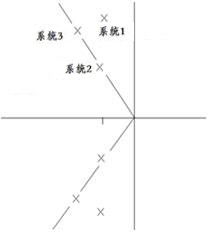
G = tf(num, den);

step(G);

hold on; % 保持当前图形，以便在同一图形中绘制多条曲线

阻尼比的影响

阻尼比(zeta)决定了系统的稳定性和响应速度。当(zeta)增大时，系统的超调量减小，但上升时间可能变长。以下是一个示例代码，展示了不同(zeta)值对阶跃响应的影响：

```matlab

% 定义不同阻尼比

zeta_values = [0.1, 0.5, 0.9];

% 循环绘制阶跃响应曲线

for i = 1:length(zeta_values)

zeta = zeta_values(i);

num = wn^2;

den = [1 2zetawn wn^2];

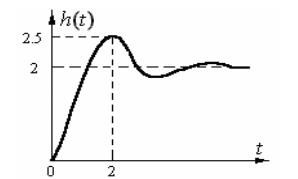
G = tf(num, den);

step(G);

hold on; % 保持当前图形，以便在同一图形中绘制多条曲线

结论

本文利用MATLAB软件对二阶系统的阶跃响应进行了分析，探讨了系统参数对响应的影响。通过仿真实验，我们可以直观地观察到不同参数对系统性能的影响，为实际工程应用提供参考。

二阶系统，阶跃响应，MATLAB，无阻尼自然频率，阻尼比